Lösung zu Aufgabe 1 (Zufallsversuche)
In einer Urne befinden sich 2 rote und 4 blaue Kugeln. Es wird zweimal mit Zurücklegen gezogen.
- Zeiche das Baumdiagramm zu diesem Versuch.
- Gib die Ergebnismenge an.
- Berechne die Ergebniswahrscheinlichkeiten.
- Berechne die Wahrscheinlichkeit, mindestens eine rote Kugel zu ziehen.
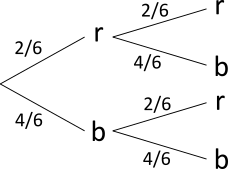Man kann nur entweder eine rote oder eine blaue Kugel ziehen. Dabei ist die Pfadwahrscheinlichkeit einer roten Kugel
$p(r) = 2 / 6$, da es zwei rote von insgesamt 6 Kugeln gibt. Die Pfadwahrscheinlichkeit einer blauen Kugel ist dann
entsprechend $p(b) = 4 / 6$.
Ziehen mit Zurücklegen heißt, dass sich die Anzahl der Kugeln nicht verändert, wenn ein zweites Mal gezogen wird.
Die Ergebnismenge ist dann $$ \Omega = \{ rr ; rb ; br ; bb \} $$
Die Ergebniswahrscheinlichkeiten lassen sich mit der ersten Pfadregel berechnen: \begin{align} P(rr) &= \frac26 \cdot \frac26 = \frac{4}{36} = \frac19 \\ \\ P(rb) &= \frac26 \cdot \frac46 = \frac{8}{36} = \frac29 \\ \\ P(br) &= \frac46 \cdot \frac26 = \frac{8}{36} = \frac29 \\ \\ P(bb) &= \frac46 \cdot \frac46 = \frac{16}{36} = \frac49 \end{align}
Das Ereignis $E = \text{ mind. eine rote Kugel}$ beinhaltet die Ergebnisse $\{rr\}; \{rb\}; \{br\}$. Die Wahrscheinlichkeit für das Ereignis ist dann mit der zweiten Pfadregel: \begin{align} P(E) &= P(rr) + P(rb) + P(br) \\ \\ P(E) &= \frac19 + \frac29 + \frac29 \\ \\ P(E) &= \frac59 = 0,556 \end{align}
Eine Alternative wäre die Bestimmung des Gegenereignisses $\bar{E} = \text{ keine rote Kugel}$. Das umfasst lediglich das Ergebnis $\{bb\}$. Die gesuchte Wahrscheinlichkeit ergibt sich dann: \begin{align} P(E) &= 1 - P(\bar{E}) \\ \\ P(E) &= 1 - \frac49 \\ \\ P(E) &= \frac59 \end{align}
Je nachdem, was günstiger ist, empfiehlt es sich, den einen oder den anderen Weg zu gehen.